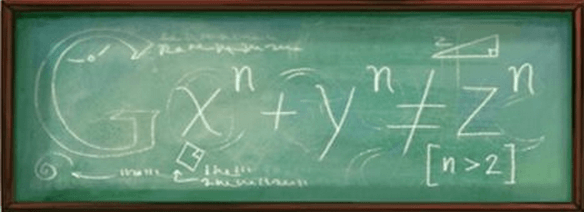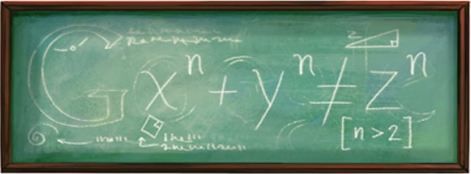Vandaag is het 414 jaar geleden dat de Franse wiskundige Pierre de Fermat geboren werd. Waarschijnlijk hebben veel mensen wel eens van “De stelling van Fermat” gehoord:
Eén blik op de beruchte formule is weer voldoende om mijn brein aan het werk te zetten om de ogenschijnlijk eenvoudige stelling zelf dan maar eens te bewijzen.
Wat maakt deze stelling zo fascinerend dat er prachtige boeken en films over gemaakt zijn? Fermat heeft in de 1637 in de kantlijn van een exemplaar van een Grieks wiskundeboek (Arithmetica) de -ogenschijnlijk eenvoudige- stelling die in de afbeelding te zien is geschreven en er bij gekrabbeld dat hij een “waarlijk schitterend” bewijs voor deze stelling gevonden heeft, maar dat de marge te klein was om deze daar op te schrijven. Dit heeft geleid tot een obsessieve zoektocht naar het bewijs voor deze stelling met als meest bekende hoogtepunt de 7 jaar die de Engelsman Andrew Wiles in alle eenzaamheid heeft doorgebracht om tot zijn bewijs te komen.
Ook eens proberen? Wanneer je n=2 invult, krijg je “gewoon” de stelling van Pythagoras. Er zijn dan meerdere oplossingen (bijvoorbeeld: x=3, y=4, z=5) waarbij de stelling klopt. De uitdaging is om een geheel getal, groter dan 2 te vinden, waarvoor de stelling blijft kloppen wanneer je een geheel getal, groter dan 0, voor a, b en c invult.